Bias Variance Tradeoff
TL;DR
| Resaon | Example | affect | Model’s complexity ⬆️ | Model’s complexity ⬇️ | |
|---|---|---|---|---|---|
| Bias | wrong assumption | assume a quadratic model to be linear | underfitting | ⬇️ | ⬆️ |
| Variance | excessive sensitivity to small variations | high-degree polynomial model | overfitting | ⬆️ | ⬇️ |
| Inreducible error | noisy data |
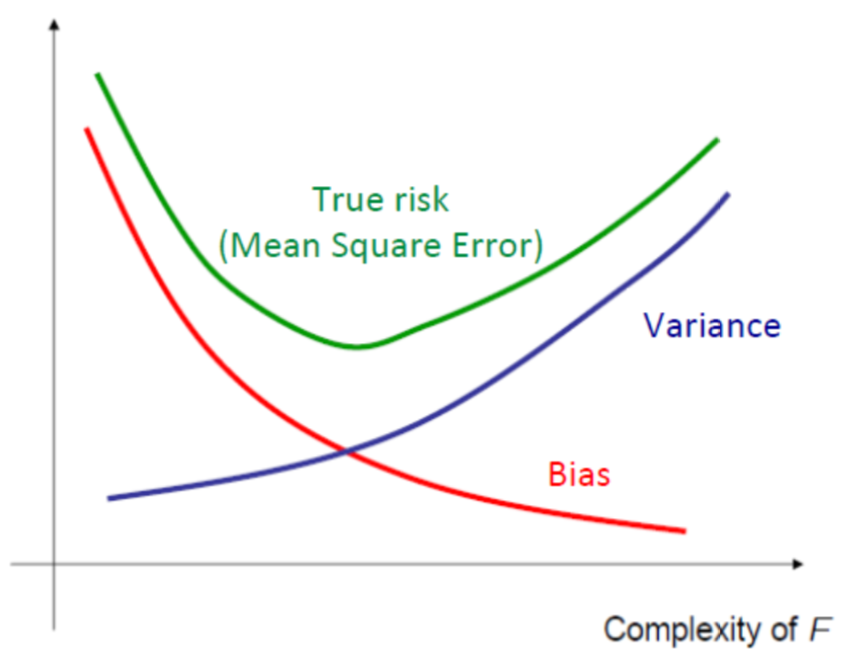
Explaination
A model’s generalization error can be expressed as the sum of three very different errors:
Bias
This part of the generalization error is due to wrong assumptions, such as assuming that the data is linear when it is actually quadratic. A high-bias model is most likely to underfit the training data.
Variance
This part is due to the model’s excessive sensitivity to small variations in the training data.
A model with many degrees of freedom (such as a high-degree polynomial model) is likely to have high variance, and thus to overfit the training data.
Irreducible Error
This part is due to the noisiness of the data itself. The only way to reduce this part of the error is to clean up the data (e.g., fix the data sources, such as broken sensors, or detect and remove outliers).
| High bias | Low bias | |
|---|---|---|
| High variance | something is terribly wrong! 😭 | Overfitting |
| Low variance | Underfitting | too good to be true! 🤪 |